lunes, 23 de diciembre de 2013
martes, 17 de diciembre de 2013
Vídeos Poliedros
- http://www.youtube.com/watch?
v=BqGFYZmd4aA&feature=plcp - http://www.youtube.com/watch?v=Ur5OObjXz_0&feature=plcp
- http://www.youtube.com/watch?
v=1MI_P2DRjr8&feature=plcp - http://www.youtube.com/watch?v=rRXgo5C0WX8&feature=plcp
- http://www.youtube.com/watch?
NR=1&v=H7qE_Tc8e4g&feature= endscreen - http://www.youtube.com/watch?v=xdpk9dlsdMU
- http://www.youtube.com/watch?
v=fWE2sq_HZvc
lunes, 2 de diciembre de 2013
Sucesión de Fibonacci y otras sucesiones
- ¡La clave está en los conejitos!
- Aplicaciones sucesiones
- A la biología
- Aplicaciones (problemas) de las sucesiones aritméticas
- Aplicaciones (problemas) de las sucesiones geométricas
- Otras aplicaciones:
- Además las sucesiones tienen que ver con el "concepto de función" (las sucesiones "son funciones" en las que sólo se pueden poner como x a números naturales) y con el "concepto de límite". ¿No te apetecería investigar por ahí?
jueves, 28 de noviembre de 2013
Paradoja de Zenón - Sucesiones
¿Sirven las sucesiones para algo?
¡¡Por lo menos para volvernos locos!!
No te lo crees, mira:
Y lee...
http://catedu.es/matematicas_mundo/HISTORIA/historia_Zenon.htm
http://www.neoteo.com/las-paradojas-de-zenon/
jueves, 14 de noviembre de 2013
Matemáticas y Literatura - Chéjov
El gran escritor ruso, Chéjov, en uno de sus maravillosos relatos, hace uso de las matemáticas para describir cierto momento.
¡Léelo aquí!
¡Léelo aquí!
martes, 29 de octubre de 2013
0.99999.... = 1 !!!! (Pero..., ¿estamos locos o qué?)
Fuente: http://www.eliax.com/index.cfm?post_id=8184
He aquí una de las pruebas matemáticas más asombrosas que incluso a los más experimentados en matemáticas deja perplejos (y que acá podrá entender cualquier persona que sepa lo más básico del álgebra): El número 0.9999... es idéntico al número 1.
He aquí la prueba desde dos puntos de vistas distintos:
Como pueden observar, literalmente el número aparentemente infinito 0.9999999... es en realidad el número 1. Y no solo eso, sino que esto ha sido demostrado utilizando todo tipo de formas matemáticas y herramientas, inclusive con formas de números alternativos.
El truco está en entender que existe más de una forma de representar un número, y que lo que vemos como 0.999999999... no es más que un símbolo que representa en realidad el número 1.
Pero no crean que por simplemente yo escribir el párrafo anterior que soy ningún genio matemático, a mí mismo este dato me dejó tan sorprendido la primera vez que lo vi como estoy seguro los dejará a varios de ustedes ahora mismo, en particular los aficionados a las matemáticas que nunca vieron esto antes, y que sin duda (como traté de hacerlo yo) tratarán de encontrar algún "truco" que invalide esto en las pruebas acá presentadas... :)
Lean más respecto a este tema en este enlace en Wikipedia en inglés
He aquí una de las pruebas matemáticas más asombrosas que incluso a los más experimentados en matemáticas deja perplejos (y que acá podrá entender cualquier persona que sepa lo más básico del álgebra): El número 0.9999... es idéntico al número 1.
He aquí la prueba desde dos puntos de vistas distintos:
Prueba por fracciones y división larga: 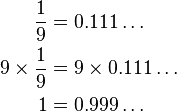 | Prueba por manipulación de dígitos: 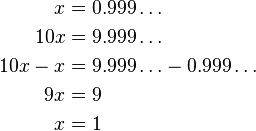 |
Como pueden observar, literalmente el número aparentemente infinito 0.9999999... es en realidad el número 1. Y no solo eso, sino que esto ha sido demostrado utilizando todo tipo de formas matemáticas y herramientas, inclusive con formas de números alternativos.
El truco está en entender que existe más de una forma de representar un número, y que lo que vemos como 0.999999999... no es más que un símbolo que representa en realidad el número 1.
Pero no crean que por simplemente yo escribir el párrafo anterior que soy ningún genio matemático, a mí mismo este dato me dejó tan sorprendido la primera vez que lo vi como estoy seguro los dejará a varios de ustedes ahora mismo, en particular los aficionados a las matemáticas que nunca vieron esto antes, y que sin duda (como traté de hacerlo yo) tratarán de encontrar algún "truco" que invalide esto en las pruebas acá presentadas... :)
Lean más respecto a este tema en este enlace en Wikipedia en inglés
Números Romanos
Nos faltaba por ver en clase cómo se escribía 4000 y 5000:
4000: IV
5000: V
Ya de paso os dejo cómo se escriben los números romanos del 1 al 5000:
Además.... Mira:
Para números con valores igual o superiores a 4000, se coloca una línea horizontal por encima del número, para indicar que la base de la multiplicación es por 1000:
(solo que aqui no sale la rayita encima)
Romano (miles) Decimal Nominación
IV.... 4000......cuatro mil con una rayita encima de IV
V..... 5000 ......cinco mil con una rayita encima del V
VI ....6000 .....con una rayita encima del VI
X.... 10000 diez mil
L..... 50000 cincuenta mil
C.... 100000 cien mil
D.... 500000 quinientos mil
M....1000000 un millón
(recuerda que estos que te puse llevan rayita arriba pero aqui no sale)
El valor de los números romanos queda multiplicado por mil tantas veces como rayas horizontales se coloquen encima de los mismos. Ejemplos: = M (con una rayita arriba) es 1.000.000
Un saludo.
4000: IV
5000: V
Ya de paso os dejo cómo se escriben los números romanos del 1 al 5000:
Además.... Mira:
Para números con valores igual o superiores a 4000, se coloca una línea horizontal por encima del número, para indicar que la base de la multiplicación es por 1000:
(solo que aqui no sale la rayita encima)
Romano (miles) Decimal Nominación
IV.... 4000......cuatro mil con una rayita encima de IV
V..... 5000 ......cinco mil con una rayita encima del V
VI ....6000 .....con una rayita encima del VI
X.... 10000 diez mil
L..... 50000 cincuenta mil
C.... 100000 cien mil
D.... 500000 quinientos mil
M....1000000 un millón
(recuerda que estos que te puse llevan rayita arriba pero aqui no sale)
El valor de los números romanos queda multiplicado por mil tantas veces como rayas horizontales se coloquen encima de los mismos. Ejemplos: = M (con una rayita arriba) es 1.000.000
Un saludo.
El Hombre que Calculaba - El problema de los camellos
Seguramente que el personaje de estas historias debió ser un contador público para ser tan ágil para cuadrar los números, no según la exactitud y rigurosidad matemática sino con base al resultado que se esperado.
Donde se narra la singular aventura de los treinta y cinco camellos que tenían que ser repartidos entre tres hermanos árabes. Cómo Beremiz Samir, el Hombre que Calculaba, efectuó un reparto que parecía imposible, dejando plenamente satisfechos a los tres querellantes. El lucro inesperado que obtuvimos con la transacción.

Hacía pocas horas que viajábamos sin detenernos cuando nos ocurrió una aventura digna de ser relatada, en la que mi compañero Beremiz, con gran talento, puso en práctica sus habilidades de eximio cultivador del Álgebra.
Cerca de un viejo albergue de caravanas medio abandonado, vimos tres hombres que discutían acaloradamente junto a un hato de camellos.
Cerca de un viejo albergue de caravanas medio abandonado, vimos tres hombres que discutían acaloradamente junto a un hato de camellos.
Entre gritos e improperios, en plena discusión, braceado como posesos, se oían exclamaciones:
-¡Que no puede ser!
-¡Es un robo!
-¡Pues yo no estoy de acuerdo!
-¡Que no puede ser!
-¡Es un robo!
-¡Pues yo no estoy de acuerdo!
El inteligente Beremiz procuró informarse de lo que discutían.
-Somos hermanos, explicó el más viejo, y recibimos como herencia esos 35 camellos. Según la voluntad expresa de mi padre, me corresponde la mitad, a mi hermano Hamed Namur una tercera parte y a Harim, el más joven, solo la novena parte. No sabemos, sin embargo, cómo efectuar la partición y a cada reparto propuesto por uno de nosotros sigue la negativa de los otros dos. Ninguna de las particiones ensayadas hasta el momento, nos ha ofrecido un resultado aceptable. Si la mitad de 35 es 17 y medio, si la tercera parte y también la novena de dicha cantidad tampoco son exactas ¿cómo proceder a tal partición?
-Muy sencillo, dijo el Hombre que Calculaba. Yo me comprometo a hacer con justicia ese reparto, mas antes permítanme que una a esos 35 camellos de la herencia este espléndido animal que nos trajo aquí en buena hora.
En este punto intervine en la cuestión.
-Muy sencillo, dijo el Hombre que Calculaba. Yo me comprometo a hacer con justicia ese reparto, mas antes permítanme que una a esos 35 camellos de la herencia este espléndido animal que nos trajo aquí en buena hora.
En este punto intervine en la cuestión.
-¿Cómo voy a permitir semejante locura? ¿Cómo vamos a seguir el viaje si nos quedamos sin el camello?
-No te preocupes, bagdalí, me dijo en voz baja Beremiz. Sé muy bien lo que estoy haciendo. Cédeme tu camello y verás a que conclusión llegamos.
-No te preocupes, bagdalí, me dijo en voz baja Beremiz. Sé muy bien lo que estoy haciendo. Cédeme tu camello y verás a que conclusión llegamos.
Y tal fue el tono de seguridad con que lo dijo que le entregué sin el
menor titubeo mi bello jamal, que, inmediatamente, pasó a
incrementar la cáfila que debía ser repartida entre los tres herederos.
-Amigos míos, dijo, voy a hacer la división justa y exacta de los camellos, que como ahora ven son 36.
Y volviéndose hacia el más viejo de los hermanos, habló así:
-Tendrías que recibir, amigo mío, la mitad de 35, esto es: 17 y
medio. Pues bien, recibirás la mitad de 36 y, por tanto, 18. Nada tienes que reclamar puesto que sales ganando con esta división.
Y dirigiéndose al segundo heredero, continuó:
-Y tú, Hamed, tendrías que recibir un tercio de 35, es decir 11 y
poco más. Recibirás un tercio de 36, esto es, 12. No podrás protestar, pues también tú sales ganando en la división.
Y por fin dijo al más joven:
-Y tú, joven Harim Namur, según la última voluntad de tu padre,
tendrías que recibir una novena parte de 35, o sea 3 camellos y parte del otro. Sin embargo, te daré la novena parte de 36 o sea, 4. Tu ganancia será también notable y bien podrás agradecerme el resultado.
Y concluyó con la mayor seguridad:
-Por esta ventajosa división que a todos ha favorecido,
corresponden 18 camellos al primero, 12 al segundo y 4 al tercero, lo que da un resultado – 18 + 12 + 4 – de 34 camellos. De los 36 camellos sobran por tanto dos. Uno, como saben, pertenece al badalí, mi amigo y compañero; otro es justo que me corresponda, por haber resuelto a satisfacción de todos el complicado problema de la herencia.
-Eres inteligente, extranjero, exclamó el más viejo de los tres hermanos, y aceptamos tu división con la seguridad de que fue hecha con justicia y equidad.
Y el astuto Beremiz –el Hombre que Calculaba- tomó posesión de
uno de los más bellos jamales del hato, y me dijo entregándome por
la rienda el animal que me pertenecía:
menor titubeo mi bello jamal, que, inmediatamente, pasó a
incrementar la cáfila que debía ser repartida entre los tres herederos.
-Amigos míos, dijo, voy a hacer la división justa y exacta de los camellos, que como ahora ven son 36.
Y volviéndose hacia el más viejo de los hermanos, habló así:
-Tendrías que recibir, amigo mío, la mitad de 35, esto es: 17 y
medio. Pues bien, recibirás la mitad de 36 y, por tanto, 18. Nada tienes que reclamar puesto que sales ganando con esta división.
Y dirigiéndose al segundo heredero, continuó:
-Y tú, Hamed, tendrías que recibir un tercio de 35, es decir 11 y
poco más. Recibirás un tercio de 36, esto es, 12. No podrás protestar, pues también tú sales ganando en la división.
Y por fin dijo al más joven:
-Y tú, joven Harim Namur, según la última voluntad de tu padre,
tendrías que recibir una novena parte de 35, o sea 3 camellos y parte del otro. Sin embargo, te daré la novena parte de 36 o sea, 4. Tu ganancia será también notable y bien podrás agradecerme el resultado.
Y concluyó con la mayor seguridad:
-Por esta ventajosa división que a todos ha favorecido,
corresponden 18 camellos al primero, 12 al segundo y 4 al tercero, lo que da un resultado – 18 + 12 + 4 – de 34 camellos. De los 36 camellos sobran por tanto dos. Uno, como saben, pertenece al badalí, mi amigo y compañero; otro es justo que me corresponda, por haber resuelto a satisfacción de todos el complicado problema de la herencia.
-Eres inteligente, extranjero, exclamó el más viejo de los tres hermanos, y aceptamos tu división con la seguridad de que fue hecha con justicia y equidad.
Y el astuto Beremiz –el Hombre que Calculaba- tomó posesión de
uno de los más bellos jamales del hato, y me dijo entregándome por
la rienda el animal que me pertenecía:
-Ahora podrás, querido amigo, continuar el viaje en tu camello, manso y seguro. Tengo otro para mi especial servicio. Y seguimos camino hacia Bagdad.
Tomado del libro “El hombre que calculaba” de Malba Tahan. Fuente: http://www.gerencie.com/distribucion-de-35-camellos-entre-tres-personas.html
PREGUNTA: ¿SABES EXPLICAR LO QUE HA PASADO?
La Soledad de los Números Primos
La Soledad de los Números Primos
Este primer texto es un fragmento del libro "La soledad de los números primos", libro escrito por un físico en el que, sin ser la ciencia el hilo conductor, el escritor hace metáforas y comparaciones con fenómenos físicos o matemáticos que hacen al lector con nociones de la Ciencia verla en situaciones bien cotidianas:
"Los números primos sólo son exactamente divisibles por 1 y por sí mismos. Ocupan su sitio en la infinita serie de los números naturales y están, como todos los demás, emparedados entre otros dos números, aunque ellos más separados entre sí. Son números solitarios, sospechosos, y por eso encantaban a Mattia, que unas veces pensaba que en esa serie figuraban por error, como perlas ensartadas en un collar, y otras veces que también ellos querrían ser como los demás, números normales y corrientes, y que por alguna razón no podían. Esto último lo pensaba sobre todo por la noche, en ese estado previo al sueño en que la mente produce mil imágenes caóticas y es demasiado débil para engañarse a sí misma.
En primer curso de la universidad había estudiado ciertos números primos más especiales que el resto, y a los que los matemáticos llaman primos gemelos: son parejas de primos sucesivos, o mejor, casi sucesivos, ya que entre ellos siempre hay un número par que les impide ir realmente unidos, como el 11 y el 13, el 17 y el 19, el 41 y el 43. Si se tiene paciencia y se sigue contando, se descubre que dichas parejas aparecen cada vez con menos frecuencia. Lo que encontramos son números primos aislados, como perdidos en ese espacio silencioso y rítmico hecho de cifras, y uno tiene la angustiosa sensación de que las parejas halladas anteriormente no son sino hechos fortuitos, y que el verdadero destino de los números primos es quedarse solos. Pero cuando, ya cansados de contar, nos disponemos a dejarlo, topamos de pronto con otros dos gemelos estrechamente unidos. Es convencimiento general entre los matemáticos que, por muy atrás que quede la última pareja, siempre acabará apareciendo otra, aunque hasta ese momento nadie pueda predecir dónde.
Mattia pensaba que él y Alice eran eso, dos primos gemelos solos y perdidos, próximos pero nunca juntos. A ella no se lo había dicho. Cuando se imaginaba confiándole cosas así, la fina capa de sudor que cubría sus manos se evaporaba y durante los siguientes diez minutos era incapaz de tocar nada. "
Paolo Giordano, "La soledad de los números primos".
Suscribirse a:
Comentarios (Atom)
